阻抗性能深入剖析
我们都记得欧姆定律和电阻的定义,它是用来表征电路阻碍电流通过的能力。可是这个非常有用的欧姆定律只适用于一个电路元件,并且假定它是一个理想电阻。实际的电路电阻要比理想电阻复杂得多,并且呈现出阻性、容性和感性特性,它们一起决定了其阻抗特性。阻抗与电阻不同点在于两个主要方面。首先,阻抗是一种交流(AC)特性;其次,通常在某个特定频率下定义阻抗。如果在不同的频率条件下测量阻抗,会得到不同的阻抗值。通过测量多个频率下的阻抗,才可能获取有价值的元件数据。这就是阻抗频谱法(IS)的基础,也是为许多工业、仪器仪表和汽车传感器应用打下基础的基本概念。
电子元件的阻抗可由电阻器、电容器和电感器组成,或者更一般的情况是三者的组合。可以采用虚数阻抗来建立这种模型。电感器具有的阻抗为jωL,电容器具有的阻抗为1 / jωC,其中j是虚数单位,ω是信号的角频率。采用复数运算将这些阻抗分量组合起来。阻抗的虚数部分称为电抗,总表达式为Z = R + jX,其中X为电抗,Z表示阻抗。当信号的频率上升时,容抗XC降低,而感抗XL升高,从而引起总阻抗的变化,阻抗与频率呈函数关系。纯电阻的阻抗不随频率变化。
如何分析阻抗
为了检查以不同的频率扫描待测测元件的阻抗,通常需要测量时域或频域响应信号。测量频域响应信号通常采用模拟信号分析方法,例如交流(AC)耦合电桥,但是高性能模数转换器(ADC)的出现允许在时域采集数据,然后再转换到频域。
许多积分变换都可以用于将数据转换到频域,例如傅里叶分析是一种很常见的方法。这种方法就是取出一系列时域信号表示,然后应用积分变换将其映射为频谱。采用这种方法可以给出任意两种信号之间关系的数学描述。在阻抗分析中感兴趣的是激励电流(元件的输入)和电压响应(元件的输出)之间的关系。如果系统是线性的,测得的时域电压和电流的各自傅里叶变换的比值就等于其阻抗,并且它可以表示成一个复数。这个复数的实数部分和虚数部分构成随后数据分析的关键部分。

其中
E = 系统电压
I = 系统电流
t = 时域参数 ![]() = 傅里叶变换
= 傅里叶变换
将复数形式转换成极坐标形式便可以得到在特定频率下响应信号的幅度和相位与激励信号的关系。


其中R和X分别表示复数的实部和虚部。上面计算得到的幅度表示该元件在特定频率条件下的复数阻抗。在扫频的情况下,可以计算出每个频率点对应的复数阻抗。
阻抗数据分析
常用的方法是将产生的阻抗与频率的关系曲线作为数据分析的一部分。当频率在给定的范围内扫频时,奈奎斯特(Nyquist)图是在复数平面内以传递函数的实部和虚部为参数的曲线。如果图中的x轴表示实部,y轴表示虚部(注意:y轴取负数),就可以得到每个频率点的阻抗表示。换句话说就是,曲线上的每个点都代表了某个频率点的阻抗。可以从向量长度|Z|计算出阻抗,该向量与x轴之间的夹角为Ø。图1示出了电阻器和电容器并联时的典型奈奎斯特图。
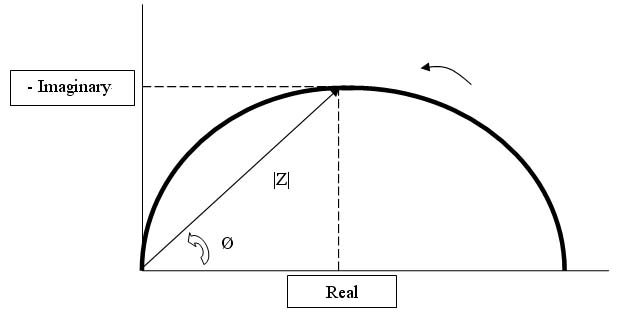
图1. 电阻器和电容器并联时的奈奎斯特图
另外一种常用的表示方法就是波特(Bode)图。在波特图中,x轴表示频率的对数,阻抗的幅度绝对值|Z|和相角都用y轴表示。因此波特图同时表示了阻抗与频率和相角与频率的关系。通常将奈奎斯特图和波特图一起使用来分析传感器元件的传递函数。
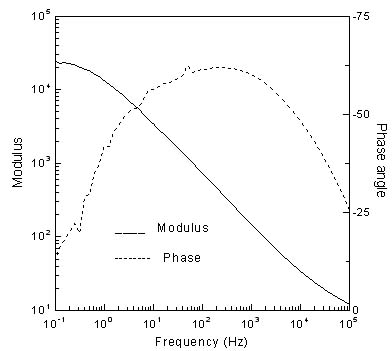
图2. 表示阻抗与频率和相角与频率之间关系的波特曲线
基于阻抗特性的传感器
考虑一个基于阻抗特性的传感器,在正常条件下根据其电容、电感和电阻特性的组合情况会产生一个特定的阻抗信号。如果传感器周围环境的变化引起上述特性的任何变化,结果都会造成阻抗的改变。通过测量这种阻抗传感器随频率变化得到的一系列新的阻抗特性将会产生由此变化的相应结果。
一种相当简单的方法就是将阻抗的测量值和预测值比较以便得出某种结论。按照这种工作原理的一个实例就是一种采用涡流原理的金属检测传感器。因为在位于传感器外壳的线圈中产生一个高频AC信号。该线圈产生的电磁场在导电靶中感应出涡流。从而这个涡流与该传感器线圈相互作用,所以改变了其阻抗。
测量线圈阻抗随频率变化的能力可提供许多好处。因为材料的渗透率会影响线圈的阻抗,所以利用经验阻抗特性可得出某些有关金属类型的结论。采用这种方法还可以用来允许该阻抗特性传感器检测具有不同渗透率的金属。渗透率变化还可以用于测量金属压力,因为压力变化会改变渗透率,而渗透率的变化又会改变阻抗。波特图和奈奎斯特图在检查传感器的频率响应方面是很有用的。测量大量频率点的阻抗比测量单个频率点的阻抗得到的结果精确,因为它有助于通过平均去掉噪声。它还通过在某些特定条件下测量电容分量和电感分量的频率响应确定出最佳的工作频率点。
将阻抗的测量值和其理想值相比较的方法可适用于许多不同的基于阻抗特性能引起电阻、电容或电感变化的传感器技术。常见的应用范围包括从采用化学传感器的气体检测、基于电容特性的湿度传感器、游戏或食品业中的金属硬币或颗粒特征识别,一直到农业中的土壤监测。
不仅是一种传感器
阻抗分析可包含极其简单地将阻抗响应特性与其理想特性相比较。阻抗频谱法(IS)也通常习惯用于表征系统以及获取有关系统的有价值信息。本文的目的是将系统从总体上定义为一个元件或者与电极有电接触的材料。这种接触可以是固体与固体(在许多化学传感器的情况下)或者固体与液体(当测量液体中某种成分的浓度时)之间的界面。采用IS可以得到有关元件本身和元件与电极之间界面的信息。
IS的原理利用这样的事实:如果给界面施加很小的电位,它就会极化。按照界面极化与当施加电位倒相时能改变电化学反应的速率相结合的方法表征界面的特性。对于系统界面,例如吸附和反应速率常数、扩散系数和电容等信息都可以得到。对于元件本身有关其介电常数、电导率、电荷均衡迁移率、各成分浓度以及大的生成率和复合率等信息都可以估计出来。
系统或元件的等效电路模型是分析阻抗扫描所产生数据的基础。这种模型通常是所连接的电阻器、电容器和电感器的组合以便模拟该系统的电特性。我们要找的模型就是在不同频率下其阻抗要与测得的阻抗特性相匹配。在理想情况下,选择模型的元件和互连方式以表示特定的电化学特性,而且要基于该过程的物理特性。可以采用文献中已有的模型,也可以根据经验建立一种模型。
在根据经验建立模型的情况下,要在经验模型和测量数据之间找到最佳匹配。因为模型中的元件不一定总是符合电化学过程的物理特性,所以可以单独构建模型以便得到最佳匹配。通过逐步增大或减小元件的阻抗直至得到最佳匹配,便可以建立起经验模型。通常根据非线性最小二乘法匹配(NLLS)算法原理来完成模型的建立。借助于计算机,利用NLLS算法先初步估计模型参数,然后逐步改变每个模型参数,最后得到最佳匹配结果。采用软件叠迭代处理直至找到可以接受的最佳匹配结果。
数据分析和等效电路模型都应当非常小心对待,而且要进行尽可能多的模型验证。虽然通过增加元件数量几乎总可以建立一个非常合适的模型,但是这样并不能认为它就代表了系统的电化学过程。一般说来,经验模型应该采用尽可能少的元件,而且应当尽可能采用基于系统电化学过程理论基础的物理模型。
另外,通常可以建立具有相同阻抗特性的许多不同的经验模型。虽然有可能得到一个很好的最小二乘法匹配模型,但是它仍然有一个不能代表该物理系统的不恰当模型。还有可能NLLS拟合算法或者对测量特性有漏掉的部分或者没有收敛。这是因为很多算法都试图在整个频谱范围内优化拟合曲线,所以有可能漏掉了频谱中某些特定频率点不好的拟合数据。
腐蚀分析是采用IS法表征系统特性的常见应用,也是一个很好的实例。金属的腐蚀(例如铝和钢)是许多行业中的重大安全考虑因素。如果不重视的话,它可以导致过早损失。自动监视腐蚀的能力能显著节省成本,具有安全和可靠性优势,而且有助于最佳化预防性地维护系统。
除了确定腐蚀的程度,通过监测腐蚀的速率还有可能预测金属疲劳。产生金属疲劳后,在小裂缝出现的地方会从有弹性变为没有弹性。这些裂缝是新的,但是腐蚀速率相当地快,而且裂纹扩展的速率以及并发的腐蚀代表了金属疲劳的程度。早期鉴定腐蚀的方法,特别是在无法看到的很难达到的位置,可以防止或者减慢严重腐蚀的破坏。它还可以用于帮助在现实条件下鉴定不同的保护涂层。
下面是根据物理学知识和腐蚀期间发生的电化学过程建立的一种腐蚀过程等效电路模型。常用于腐蚀监视的等效电路用一个电阻器(Rp)和电容器(Cp)相并联再与一个电阻器Rs相串联表示。
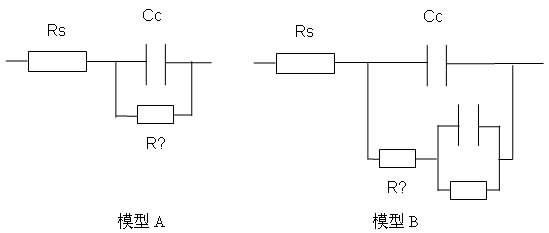
图3. 用于腐蚀分析的常用等效电路
在模型A中电阻器Rs表示金属所在的溶液,而电容Cc表示金属表面的保护涂层或涂料。这表示初始涂层的电容。经过一段时间后,水渗入涂层中形成新的液体和金属界面。随着金属的腐蚀,穿过溶液与金属之间的保护涂层形成离子导电路径。这可以用R? 与Cc并联模型表示来。另外,有些模型(模型B)还有一个附加的R和C并联起来再与R?串联来表示金属保护涂层随着时间变化的分层模型。
金属所在的溶液的电阻率或电导率通常是已知的或者很容易获得,所以可以得到Rs。还可以得到Cp的值,因为可以由保护涂层的介电常数(通常由厂商提供)及其覆盖的面积计算得到。然后就是求解R?以便确定腐蚀的程度。通常通过曲线拟合算法得到测量阻抗特性数据的最佳拟合来解决这个问题。采用波特图也是很常用的方法,它根据其阻抗频率响应和相位频率响应来检测腐蚀传感器的特性。
IS法不仅仅限于腐蚀分析,还可以用于表征多种电化学系统。例如,它可以用于优化燃料电池性能,预测电池健康状况,检查液体中某种成分的浓度以便确定其质量,还可以表征某种材料的电化学性能。
电路设计
等效电路模型一旦确定,就必须设计电子数据采集系统来完成频率扫描和获取数据。这通常是一项既复杂又费时的工作,需要不可或缺的电子学知识以便优化电路设计。
设计的电路必须能在有用的范围内以要求的分辨率产生频率扫描。在许多电化学系统中必须避免采集到的数据受到电化学过程本身的干扰。所以通常采用小的AC信号,并且还很重要的一点就是不能在系统中引入DC电位差,因为它会导致进一步的电化学反应。然后必须用ADC采集系统对激励频率的响应。在有些设计中需要两个ADC分别用于捕获激励信号和响应信号。这是很复杂的,因为需要两个ADC同步采样以便检测出信号之间的相位变化。AD5933就是一种典型的集成电路(IC)芯片,它提供可编程频率扫描发生器和集成的ADC,该ADC可以激励频率配合工作来获取响应信号。另外,整个系统必须保持线性。换句话说就是系统的总带宽必须足够而且信号大小也要足够才能得到好的测量结果,但是信号又不能太大以至于超过ADC或其它元件的量程而引起失真。因为待测元件通常具有未知的阻抗范围,所以通常最开始需要做一些反复试验法来优化系统并且确保它的线性特性。将响应信号转换为数字形式后,通常将数字信号送入计算机进行下一步的分析。最新的解决方案,例如AD5933,在送给计算机进行处理之前提取了响应信号的实部和虚部,在芯片内就完成了大量的分析。这样大大减轻了计算机的运算负担,并且提高了数据采集的质量,因为模拟信号处理电路适合与其它的功能模块配合工作。应当记住的是,尽管计算机很容易能提供4位或高于4位的结果(除非测量的模拟信号是无效的),而且注意到保证整个系统保持线性,但最终结果还是会有误差的。精心的系统设计和验证以便获得有效的测量是提高最终结果精度的关键。

